NTRU cryptosystem is a grandfather of lattice-based encryption schemes. The initial idea was due to Ajtai. His work evolved into a whole area of research with the goal of creating more practical, lattice-based cryptosystems, like the first NTRU-based encryption system and signature scheme due to Hoffstein, Pipher, Silverman, Howgrawe-Graham and Whyte.
The cryptosystem is based on polynomial rings. More precisely, the base is a problem of recovering a sparse polynomial that is a factor of a polynomial modulo \(X^n - 1\) in the polynomial ring of some finite field \(F_q\).
The article below tries to explain, in easy to understand terms, the basics of NTRU, starting from a brief explanation of what the lattice is. Future articles will introduce a more detailed view of a modern approach to building NTRU-based cryptosystems.
The lattice and related hard-problems
The picture below visualizes a lattice as points in a two-dimensional space. A lattice is defined by the origin \(O\) and base vectors \(\{b_1,b_2\}\). Every point on the lattice is represented as a linear combination of the base vectors, for example \(V=−2b_1+b_2\).
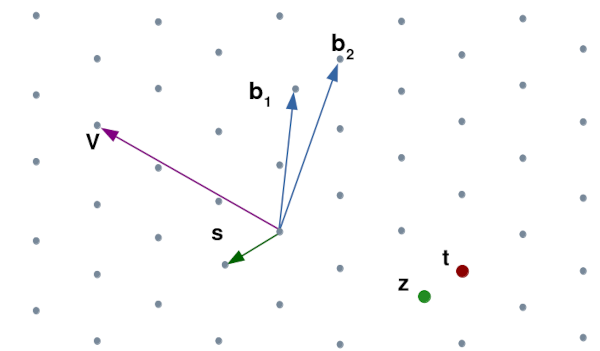 There are two classical NP-hard problems in lattice-based cryptography:
There are two classical NP-hard problems in lattice-based cryptography:
- Shortest Vector Problem (SVP): Given a lattice, to find the shortest non-zero vector in the lattice. In the graph, the vector \(s\) is the shortest one. The SVP problem is NP-hard only under some assumptions.
- Closest Vector Problem (CVP): Given a lattice and a vector \(V\) (not necessarily in the lattice), to find the closest vector to \(V\). For example, the closest vector to t is \(z\).
In the graph above, solving SVP and CVP would be quite simple. However, the lattices used in cryptography have higher dimensions, say above 1000, as well as non-orthogonal vector basis. It is believed that in these instances, the problems are hard enough to solve, even for future quantum computers.
Coppersmith and Shamir, proved in “Lattice Attacks on NTRU” (EUROCRYPT'97) that NTRU problem, can be reduced to SVP.
Rings
NTRU operates in a ring of polynomials of degree \(N\). The degree of a polynomial is the highest exponent of its variable. For example, \(x^7+6x^3+11x^2\) has degree of 7. One can add polynomials in the ring in the usual way, by simply adding theirs coefficients modulo some integer. In NTRU this integer is called as \(q\). Polynomials can also be multiplied (obviously), and the result of a multiplication is always a polynomial of degree less than \(N\). It basically means that exponents of the resulting polynomial are added to modulo \(N\). For example:
$$\begin{eqnarray} X^{N-1} \cdot X &=& X^N &=& 1 \newline X^{N-1} \cdot X^2 &=& X^{N+1} &=& X \newline X^{N-1} \cdot X^3 &=& X^{N+2} &=& X^2 \newline \dots \end{eqnarray}$$
In other words, polynomial ring arithmetic is very similar to modular arithmetic, but instead of working in a “set of numbers” less than \(N\), one works in a set of polynomials with a degree less than \(N\).
NTRU scheme: basic idea
To instantiate the NTRU cryptosystem, the following domain parameters must be chosen:
- \(N\) - degree of the polynomial ring, in NTRU the principal objects are polynomials of degree \(N−1\).
- \(p\) - small modulus, used during key generation and decryption for reducing message coefficients.
- \(q\) - large modulus, used during algorithm execution for reducing coefficients of the polynomials.
First, we generate a pair of public and private keys. To do that, two polynomials \(f\) and \(g\) are chosen from the ring in a way that their randomly generated coefficients are much smaller than \(q\). Then key generation computes two inverses of the polynomial:
$$\begin{eqnarray} f_p = f^{-1}~mod~p \newline f_q = f^{-1}~mod~q \newline \end{eqnarray}$$
The values \(f\) and \(f_p\) make up the private key. The public key \(pk\) is computed, as follows: $$\begin{eqnarray} pk = p \cdot f_q \cdot g~mod~q \end{eqnarray}$$ The \(f_q\) is not part of any key, however it must remain secret.
It might be the case that after choosing \(f\), the inverses modulo \(p\) and \(q\) do not exist. In this case, the algorithm has to start from the beginning and generate another \(f\). That’s unfortunate because calculating the inverse of a polynomial is a costly operation. The recent instantiations of some NTRU schemes (like NTRU-HRSS) are design in a way to ensure those inverses always exist. Which makes key generation faster and more reliable.
The encryption of a message \(m\) proceeds as follows. First, the message \(m\) is converted to a ring element \(pt\) (there exists an algorithm for performing this conversion in both directions). During encryption, NTRU randomly chooses one polynomial \(b\) called \(blinder\). The goal of the blinder is to generate different ciphertexts per encryption. Thus, the ciphertext \(ct\) is obtained as:
$$\begin{eqnarray} ct = (b \cdot pk + pt)~mod~q \end{eqnarray}$$
Decryption looks a bit more complicated, but it can also be easily understood. It uses both the secret value \(f\) and \(f_p\). To recover the plaintext as: $$\begin{eqnarray} v &=& f \cdot ct~mod~q \newline pt &=& v \cdot f_p~mod~p \newline \end{eqnarray}$$
Taking all that was described above, evaluation done during decryption is something like:
$$\begin{eqnarray} (f \cdot ct)&~mod~p& \cdot~f_p~mod~q= \newline (f \cdot (b\cdot pk + pt) ) &~mod~p& \cdot~f_p~mod~q= \newline (f \cdot (b\cdot f_q \cdot p \cdot g + pt) ) &~mod~p& \cdot~f_p~mod~q= \newline \xcancel{(f \cdot f_q)}(b \cdot p \cdot g) + (f \cdot pt) ) &~mod~p& \cdot~f_p~mod~q= \newline \xcancel{b \cdot g \cdot p~mod~p}+ f \cdot pt~mod~p & & \cdot~f_p~mod~q= \newline (\xcancel{f \cdot f_p}) \cdot~pt &~mod~p&~~~~~~~~mod~q=pt \end{eqnarray} $$ After obtaining \(pt\), the message \(m\) is recovered by inverting the conversion function.
The underlying hard assumption is that given two polynomials: \(f\) and \(g\) whose coefficients are short compared to the modulus \(q\), it is difficult to distinguish \(pk={f \over g}\) from a random element in the ring. It means that it’s hard to find \(f\) and \(g\) given only public key \(pk\).
Concrete schemes
The original scheme has a long (over 20 years) history. Since then it has been changed multiple times, as a response to account for cryptanalytic advances. Several variants of concrete KEM and signature schemes based on NTRU were proposed during NIST PQC standardization. In the case of KEM, two candidates NTRUEncrypt and NTRU-HRSS-KEM been merged together and end up as a scheme called … well, “NTRU”. The scheme is fairly easy to implement in constant-time with is characterized by performance, allowing it to be used in the production environment. The NTRU-based signature scheme Falcon also came to the last round of the standardization. It’s characterized by very fast execution and relatively small key sizes. Nevertheless, performance efficient, constant-time implementation can be quite complicated. It also seems, patent situation for NTRU schemes is much clearer than in case of other candidates.